Ising Model

The model used to explain this phenomenon is called the Ising Model: all the micro-magnets represent the spin of the atoms and increasing the temperature also increases the entropy − or disorder − of the system. On the contrary, when you decrease the temperature, atoms are less agitated and tend to align their spin with their neighborhood.

More mathematically, we can prove that any system at a fixed temperature $T$ tends to minimize his free energy, given by $F = U - TS$, where $U$ is the energy of the system and S its entropy. When the temperature is low, minimizing $F$ essentially means minimizing $U$, while a high temperature increases the role of entropy, and the negative signs means $F$ will be minimized for a high entropy. The Ising model consists in having an expression for the enthalpy only taking into account interactions between each atom and its direct neighborhood (long-range interactions are neglected). This expression has to be minimum when all the spins are aligned, and maximum in the most disordered case. The simplest expression respecting those conditions is given by : \[ U = - J \sum_{i,j \: neighbors} S_i S_j \] where $S_i$ is the spin of atom $i$ (-1 for blue spin and 1 for red spin) and $J$ a couping constant.

Curie Temperature

If we call $M$ the average spin value (a number between -1 and 1, equal to -1 if all spins are blue and 1 if they are all red), it is shown experimentally that $M$ evolves as a function of temperature according to this graph: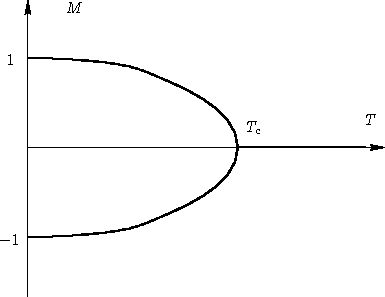 The temperature at which the magnetism becomes 0 is called Curie temperature, and defines a phase transition.

Simulation

This program simulates the Ising model using a Monte Carlo algorithm called Metropolis Algorithm, consisting essentially in mixing randomly the spins at each iteration, and accepting the new situation either if $U$ has decreased or, with a certain probability growing with the temperature, if $U$ has increased. Thus, if $T$ is high, new situations will be essentially random, while a low $T$ will make situations with low $U$ (which means aligned spins) more likely.